Thinking Inside the Box

“I feel like I’m inside my book,” says Jordan Ellenberg, here surrounded by the types of drawings he uses to explain math and its connection to daily life. Photo: Jeff Miller.
What Kinds of Mathematics Will Appear in This Book?

How Not to Be Wrong: The Power of Mathematical Thinking by Jordan Ellenberg. © 2014 by Jordan Ellenberg.
If your acquaintance with mathematics comes entirely from school, you have been told a story that is very limited, and in some important ways false. School mathematics is largely made up of a sequence of facts and rules, facts which are certain, rules which come from a higher authority and cannot be questioned. It treats mathematical matters as completely settled.
Mathematics is not settled. Even concerning the basic objects of study, like numbers and geometric figures, our ignorance is much greater than our knowledge. And the things we do know were arrived at only after massive effort, contention, and confusion. All this sweat and tumult is carefully screened off in your textbook.
There are facts and there are facts, of course. There has never been much controversy about whether 1 + 2 = 3. The question of how and whether we can truly prove that 1 + 2 = 3, which wobbles uneasily between mathematics and philosophy, is another story — we return to that at the end of the book. But that the computation is correct is a plain truth. The tumult lies elsewhere. We’ll come within sight of it several times.
Mathematical facts can be simple or complicated, and they can be shallow or profound. This divides the mathematical universe into four quadrants:
Basic arithmetic facts, like 1 + 2 = 3, are simple and shallow. So are the basic identities like sin(2x) = 2 sin x cos x or the quadratic formula: they might be slightly harder to convince yourself of than 1 + 2 = 3, but in the end they don’t have much conceptual heft.
Moving over to complicated/shallow, you have the problem of multiplying two ten-digit numbers, or the computation of an intricate definite integral, or, given a couple of years of graduate school, the trace of Frobenius on a modular form of conductor 2377. It’s conceivable you might, for some reason, need to know the answer to such a problem, and it’s undeniable that it would be somewhere between annoying and impossible to work it out by hand; or, as in the case of the modular form, it might take some serious schooling even to understand what’s being asked for. But knowing those answers doesn’t really enrich your knowledge about the world.
The complicated/profound quadrant is where professional mathematicians like me try to spend most of our time. That’s where the celebrity theorems and conjectures live: the Riemann Hypothesis, Fermat’s Last Theorem[1], the Poincaré Conjecture, P vs. NP, Gödel’s Theorem. … Each one of these theorems involves ideas of deep meaning, fundamental importance, mind-blowing beauty, and brutal technicality, and each of them is the protagonist of books of its own.
But not this book. This book is going to hang out in the upper left quadrant: simple and profound. The mathematical ideas we want to address are ones that can be engaged with directly and profitably, whether your mathematical training stops at pre-algebra or extends much further. And they are not “mere facts,” like a simple statement of arithmetic — they are principles, whose application extends far beyond the things you’re used to thinking of as mathematical. They are the go-to tools on the utility belt, and used properly they will help you not be wrong.
Pure mathematics can be a kind of convent, a quiet place safely cut off from the pernicious influences of the world’s messiness and inconsistency. I grew up inside those walls. Other math kids I knew were tempted by applications to physics, or genomics, or the black art of hedge fund management, but I wanted no such rumspringa.[2] As a graduate student, I dedicated myself to number theory, what [Carl Friedrich] Gauss called the queen of mathematics, the purest of the pure subjects, the sealed garden at the center of the convent, where we contemplated the same questions about numbers and equations that troubled the Greeks and have gotten hardly less vexing in the twenty-five hundred years since.
At first I worked on number theory with a classical flavor, proving facts about sums of fourth powers of whole numbers that I could, if pressed, explain to my family at Thanksgiving, even if I couldn’t explain how I proved what I proved. But before long I got enticed into even more abstract realms, investigating problems where the basic actors — “residually modular Galois representations,” “cohomology of moduli schemes,” “dynamical systems on homogenous spaces,” things like that — were impossible to talk about outside the archipelago of seminar halls and faculty lounges that stretches from Oxford to Princeton to Kyoto to Paris to Madison, Wisconsin, where I’m a professor now. When I tell you this stuff is thrilling, and meaningful, and beautiful, and that I’ll never get tired of thinking about it, you may just have to believe me, because it takes a long education just to get to the point where the objects of study rear into view.
But something funny happened. The more abstract and distant from lived experience my research got, the more I started to notice how much math was going on in the world outside the walls. Not Galois representations or cohomology, but ideas that were simpler, older, and just as deep — the northwest quadrant of the conceptual foursquare. …
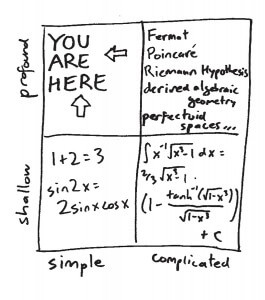
In this drawing from his book, Ellenberg explains his belief that the mathematical universe can be divided into four quadrants, and, he writes, the simple/profound quandrant offers “the go-to tools on the utility belt.”
This will not be the kind of book where I make grand, vague gestures at great monuments of mathematics, and instruct you in the proper manner of admiring them from a great distance. We are here to get our hands a little dirty. We’ll compute some things. There will be a few formulas and equations, when I need them to make a point. No formal math beyond arithmetic will be required, though lots of math way beyond arithmetic will be explained. I’ll draw some crude graphs and charts. We’ll encounter some topics from school math, outside their usual habitat; we’ll see how trigonometric functions describe the extent to which two variables are related to each other, what calculus has to say about the relationship between linear and nonlinear phenomena, and how the quadratic formula serves as a cognitive model for scientific inquiry. And we’ll also run into some of the mathematics that usually gets put off to college and beyond, like the crisis in set theory, which appears here as a kind of metaphor for Supreme Court jurisprudence and baseball umpiring; recent developments in analytic number theory, which demonstrate the interplay between structure and randomness; and information theory and combinatorial designs, which help explain how a group of MIT undergrads won millions of dollars by understanding the guts of the Massachusetts state lottery.
There will be occasional gossip about mathematicians of note, and a certain amount of philosophical speculation. There will even be a proof or two. But there will be no homework, and there will be no test.
[1] Which, among pros, is now called Wiles’s Theorem, since Andrew Wiles proved it (with a critical assist from Richard Taylor) and [Pierre de] Fermat did not. But the traditional name will probably never be dislodged.
[2]To be honest, I did spend some part of my early twenties thinking I might want to be a Serious Literary Novelist. I even finished a Serious Literary Novel, called The Grasshopper King, and got it published. But in the process I discovered that every day I devoted to Serious Literary Novel-writing was a day half spent moping around wishing I were working on math problems.
Published in the Summer 2014 issue


Comments
Edward Jakubowski June 10, 2014
I’ll have to read your book. To be honest, I was once a student to whom mathematics always came quite easily. After Martin Isaacs explained to me what life as a pure mathematician would be like, I realized I needed to spend more time working with people. I was distracted by coaching and putting teams together. I now have time to contemplate mathematics. I look forward to it.
Mary Yockey June 10, 2014
I’m sprinting out right now to get your book. Even if I may not understand it, I’ll cradle it as a baby in my arms and know that I’m holding something very precious indeed . . .
Luiz Alberto Brettas July 3, 2014
As Edward, I´ll have to read it too.
I´m a math professor at a south Brasil University.
I frequently say that studying mathematics is something like masturbation: It´s loneliness, it´s far from reality and someone can get great pleasure with it if doing the right way…
I think his book will improve my way of look at math…